Tokens and vector embeddings: The first steps in calculating semantics for LLMs

This is the second post in an ongoing series about the mechanisms behind how natural language understanding (NLU) reads content online.

For the first time, I used Claude extensively to help me define, rewrite, and fact check the concepts in this week's newsletter. Nearly every explanation of tokens and vector embeddings I've ever read is highly technical, and I have never taken a comp-sci class. Even after years of "understanding" the concepts in the back of my head, I realized my short-hand technical knowledge of "tokens=words; vector embeddings= word-shapes" was off-base. The words are my own (Claude uses too much passive voice), but the tool gave me a solid pair-writing edit.

Here's hoping Claude didn't hallucinate and misinform me, and I'm not, in turn, misinforming you. I'll include some more technical links at the end of this essay, if you want to fact check me or look into the particulars.

Tokens: Giving every word part its own special numeral

The first thing to know about "tokenization" in natural language processing is that it is quite the opposite of the "tokenism" you learned about during undergrad/ in grad school/ on South Park.* When we talk about "tokens" in cultural studies and sociology, we're talking about a situation of performative exceptionalism: the few students of color at an otherwise white college who appear in all the promotional brochures or the lone woman on a corporate executive board. When we talk about "tokens" in natural language processing, we're discussing stripping language down to its lowest common denominator and converting it to numbers, making the word anything but exceptional.

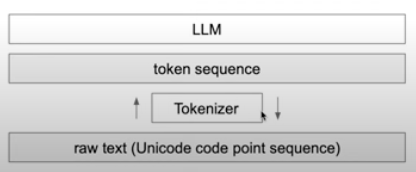
Tokenization in natural language understanding (NLU) is also different from tokenization in blockchain/web3, which describe the encryption of sensitive data. NLU tokenization is not sensitive or encrypted in any way; in LLMs, tokenization simply represents a word, a part of a word, or a character as a numeral.

But let's consider "tokenism," "tokenization (NLU)," and "tokenization (Web3)" as, well, tokens.

*I apologize, but because South Park's first season coincided with my freshman year of high school, it *was* how I was initially introduced to the term.

What is a token in natural language processing?

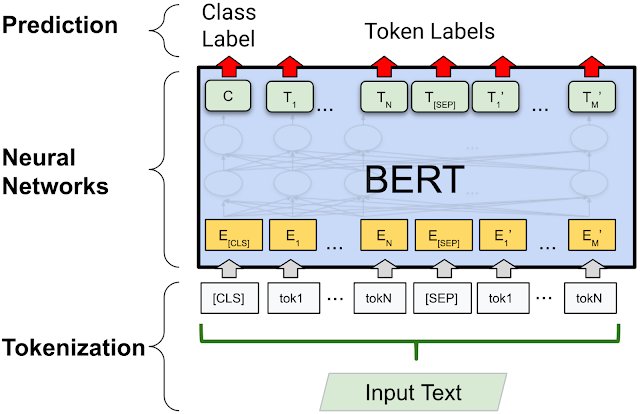
Tokenization (NLU) breaks down words into their most useful parts, so that the relationships between words can be mathematically calculated. We can tokenize whole words or individual characters, but neither of those methods is particularly efficient. What's more effective is somewhere between etymology and phonics: natural language understanding systems break down words into parts, effectively "sounding out" the word like a young reader. So:

"tokenization" > "token-" and "-ization"
"tokenism" > "token-" and "-ism"

This example breaks nicely into morphemes, or the root word and suffix. But not all tokenization is morpheme-perfect because languages are full of exceptions. From what I gather, most of the tokens used in contemporary natural language understanding are actually subword tokens, often the lowest common denominator string of letters. So:

"strategic" > "strate-" and "-gic"
"strategy" > "strate-" and "-gy"

"Strate" is not a word, nor is it a proper morpheme. It's just the common root string, or list of text characters, in a root word.

"efficient" > "efficien-" and "-t"
"efficiency" > "efficien-" and "-cy"

"Efficien-" doesn't mean anything to English-speaking humans, but to a computer trying to understand English-speaking humans, the string "efficien-" is enough to understand that the string represents a number that can be substituted for the meaning "quickly, cheaply, and with purpose."

Every string of characters is then converted into a numeral. For example:

"strate-" = 15847
"-gic" = 29384
"-gy"=18294

Thus, "strategic" tokenizes as [15847, 29384], and "strategy" tokenizes as [15847, 18294].

Tokenization is part of data pre-processing before training LLMs and essentially define an LLM's vocabulary. Models are trained on billions or trillions of tokens, and those are reduced (like a balsamic glaze) to a much smaller and more workable vocabulary. Depending on the language and the model capabilities, tokens are further compressed with technologies like Byte Pair Encoding (BPE), WordPiece, and SentencePiece.

You're likely most familiar with tokens as the input-output limits of each model. When the LLM cuts you off or tells you to wait a few hours, it's because too many tokens have been consumed.

From tokens to vectors: Making sense of words through their relationships to other words

Tokens are relatively easy to understand, but vector embeddings make the concept more complex. If you remember geometry class... well, I don't remember the role of vectors in geometry, but I remember that the entire field of geometry describes mathematical relationships represented in space. I also remember that "vectors" were part of physics, so I know vectors have something to do with how words, or tokens, relate to each other in some kind of multidimensional space.

Changing words into multidimensional representations enables computers to represent and calculate semantics. Essentially, vector embedding turns words into points in mathematical space.

In natural language understanding, vector embeddings describe relationships between multiple tokens that are semantically or contextually related. Models like Word2Vec and neural networks analyze how tokens co-occur and interact throughout a training dataset, learning common patterns and relationships among tokens. Vector embeddings are stored in a large language model's parameters, memory, and supplementary databases, enabling LLMs to encode and process semantic similarity among tokens.

If that's not crystal clear—no shame, and I'm a bit in the weeds articulating it—here's an example:

We are strategically optimizing our business for efficiency.
Efficiency powers our strategic business optimization.

Each token receives its own vector embedding——a list of numbers that represents its meaning as coordinates in multidimensional space, where semantically similar tokens are positioned closer together.

Both sentences share similar tokens, and the vector embedding describes how each tokenized word relates in space to every other token. Tokens with similar semantic relationships have vectors in close proximity to each other. In language terms, vector embeddings are great at identifying synonyms and often-paired subject-verb-object relationships.

A natural language model can understand similarity among vectors in the sentences above and understand that both sentences are about business strategy, efficiency, and optimization. They share more or less the same meaning, expressed in a slightly different form, because the vector embeddings are similar.

Context is here vector embeddings alone fall flat

But let's look at a different example:

I felt tokenized when I was the only woman speaker at the conference.
We tokenized words into subwords to process the corpus accurately.

While both sentences share one of the same words (or tokens), they mean wildly different things. In the first sentence, "tokenized" refers to "tokenism," or the feeling of being an object of performative inclusivity. In the second, "tokenized" refers to the linguistic and computational process of breaking down words, as described above.

Vector embeddings struggle with polysemy, or when the same word carries multiple meanings. The word "tokenized" would be represented with exactly the same vector embedding, even though the meaning of the word is extremely different depending on the context of the sentence.

Vector embeddings alone aren't enough to understand the complex relationships between words, sentences, and paragraphs that create meaning in language. Word2Vec was a big step toward today's LLMs, but it only tracks shallow relationships among words.

Since nearly every common term in natural language understanding has another meaning outside the field of computer science—"tokenized" being the first of many examples—NLU researchers created a mechanism to differentiate contexts. That invention, also from the researchers at Google, was the transformer, which we'll discuss next week.

Some technical explainers on tokens and vector embeddings that helped me understand what I didn't know: